数論概論学習ノート(一)——勾股数
1695 ワード
本文はブロガーのオリジナル文章で、ブロガーの許可を得ずに転載してはならない.
Pythagoras theorem
1つの直角三角形では、2つの直角辺の辺長の平方を合わせると斜辺長の平方に等しい.直角三角形の2つの直角辺の長さがそれぞれaとbであり、斜辺の長さがcである場合、数学言語で表現することができます.
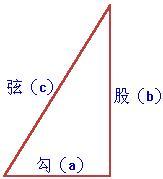
a2+b2=c2
この等式を満たしかつ公因数のない三元配列(a,b,c)を勾股数と呼ぶ.a,bの二つの数は必然的に奇異なカップルであることが証明され、以下のように証明される:a,bが奇数であれば、数cは必ず偶数である.a=2 x+1、b=2 y+1、c=2 zとすることができ、
(2x+1)2+(2y+1)2=(2z)2
展開の簡略化は次のようになります.
2x2+2x+2y2+2y+1=2z2
上式の左側は奇数で、右側は偶数で、等式は明らかに成立しない.a,bが偶数であれば,cも偶数であることを意味する.このときa,b,cはいずれも2で除去することができ,このときa,b,cは互いに質を持たない.証明書が終わりました.———
定理
a 2+b 2=c 2から得られるa 2=(c−b)(c+b)
(c+b)+(c−b)=2 cと(c+b)−(c−b)=2 b
故d 2 bと2 cを除去した.一方、b、cには公因数がない.(a,b,c)が本原勾配配列であると仮定すると、dは必ず1または2であると結論できるが、dも(c+b)(c−b)=a 2を除去し、aは奇数であるため、dは1しかないので(c−b)、(c+b)には公因数がない. 現在,c−bとc+bには公因数がなく,a 2=(c−b)(c+b)であることが分かっているので,c−b,c+bの積は平方数であり,c−bとc+b自体が平方数である場合のみである.記す
c+b=s2 ,
c−b=t2
内
s>t⩾1は、公因数のない奇数である.bとcの解方程式の組み合わせについて
c=s2+t22 ,
b=s2−t22
すると、
だから次の定理がある
a=st ,
b=s2−t22 ,
c=s2+t22 (
s>t⩾1 )
この式により,異なるs,tの値をとると,異なる勾配数を生成することができる.
下表はs
s
t
a=st
b=s2−t22
c=s2+t22
3
1
3
4
5
5
1
5
12
13
7
1
7
24
25
9
1
9
40
41
5
3
15
8
17
7
3
21
20
29
7
5
35
12
37
9
5
45
28
53
9
7
63
16
65
Pythagoras theorem
1つの直角三角形では、2つの直角辺の辺長の平方を合わせると斜辺長の平方に等しい.直角三角形の2つの直角辺の長さがそれぞれaとbであり、斜辺の長さがcである場合、数学言語で表現することができます.

a2+b2=c2
この等式を満たしかつ公因数のない三元配列(a,b,c)を勾股数と呼ぶ.a,bの二つの数は必然的に奇異なカップルであることが証明され、以下のように証明される:a,bが奇数であれば、数cは必ず偶数である.a=2 x+1、b=2 y+1、c=2 zとすることができ、
(2x+1)2+(2y+1)2=(2z)2
展開の簡略化は次のようになります.
2x2+2x+2y2+2y+1=2z2
上式の左側は奇数で、右側は偶数で、等式は明らかに成立しない.a,bが偶数であれば,cも偶数であることを意味する.このときa,b,cはいずれも2で除去することができ,このときa,b,cは互いに質を持たない.証明書が終わりました.———
定理
a 2+b 2=c 2から得られるa 2=(c−b)(c+b)
(c+b)+(c−b)=2 cと(c+b)−(c−b)=2 b
故d 2 bと2 cを除去した.一方、b、cには公因数がない.(a,b,c)が本原勾配配列であると仮定すると、dは必ず1または2であると結論できるが、dも(c+b)(c−b)=a 2を除去し、aは奇数であるため、dは1しかないので(c−b)、(c+b)には公因数がない. 現在,c−bとc+bには公因数がなく,a 2=(c−b)(c+b)であることが分かっているので,c−b,c+bの積は平方数であり,c−bとc+b自体が平方数である場合のみである.記す
c+b=s2 ,
c−b=t2
内
s>t⩾1は、公因数のない奇数である.bとcの解方程式の組み合わせについて
c=s2+t22 ,
b=s2−t22
すると、
だから次の定理がある
Pythagorean Triples Theorem:
We will get every primitive Pythagorean triple(a,b,c) with a odd and b even by using the formulas:
a=st ,
b=s2−t22 ,
c=s2+t22 (
s>t⩾1 )
この式により,異なるs,tの値をとると,異なる勾配数を生成することができる.
下表はs
s
t
a=st
b=s2−t22
c=s2+t22
3
1
3
4
5
5
1
5
12
13
7
1
7
24
25
9
1
9
40
41
5
3
15
8
17
7
3
21
20
29
7
5
35
12
37
9
5
45
28
53
9
7
63
16
65